2020년 3월에 발표된 Neural Graph Collborative Filtering 논문을 핵심적인 부분에 대해서만 정리해보려고한다.
궁금한점이나 틀린점이 있다면 언제나 태클 환영합니다!!

해당 그림은 user-item 상호작용 그래프와 해당 논문에서 강조하고 있는 high-order connectivity를 보여주는 figure이다.
오른쪽 그림은 user1을 target으로해서 user1에게 상품을 추천하기위한 figure를 나타낸다.
왼쪽 그림을 바탕으로 오른쪽 그래프를 만들 수 있다. 예를 들어서 u2 -> i2 -> u1와 같이 edge로 연결되어있는것을 방향성으로 파악해내는것이다. 즉 u1과 u2사이에는 행동 유사성이 있다고 볼 수 있다는 것이다.
또한 i4 -> u2 -> i2 -> u1을 통해 u1에게 i4를 추천해주는것이 좋다고 보는것이다. 그 이유는 u1과 u2가 유사하기 때문에 u2가 이전에 i4를 소비한 과거 기록이 존재하기 때문이다.
이러한 방식으로 해당 논문에서는 기존 CF에 비해서 high-order connectivity를 고려해서 collborative signal을 좀 더 명확히 보낼 수 있어서 성능이 좋아진다고 말하고 있다.
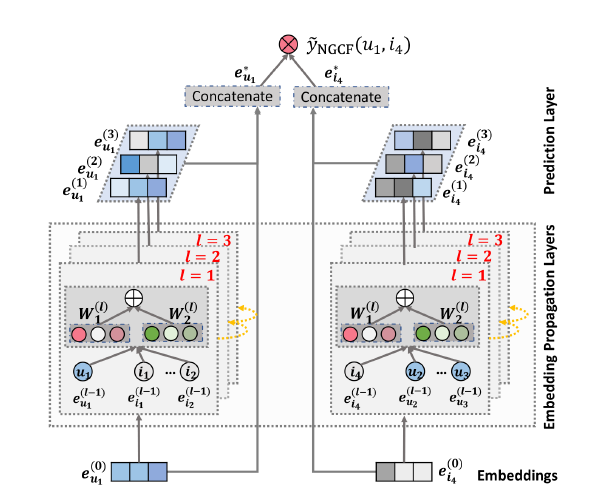
위 그림은 u1에 대한 i4의 score를 구하는 NGCF의 과정을 보여주고 있다.
- 1. Embedding Layer
- 초기값으로 각각 user와 item에 대한 User Embedding / Item Embedding을 나타내고 있다.
- 기존 MF나 NCF의 경우는 이러한 Embedding이 바로 interaction layer에 들어갔으나 NGCF에서는 직접 바로 들어가는 것이 아니라 user-item 상호작용 그래프를 바탕으로 propagate하면서 Embedding값이 전달된다. 이러한 방법을 통해 해당 논문에서는 좀더 명확한 collborative signal 전달이 가능하다고 했다.
- 2. Embedding Propogation Layer
- 위의 figure에서는 3-order로 그러져있다. 일단 1-order에 대해서 자세히 살펴보면 message construction과 message aggregation이 존재한다
- message construction은 하나의 아이템이 하나의 유저에게 전달하는 메세지이다.
- $$ {m_{u\leftarrow i}} = f({e_{i}}, {e_{m}}, {p_{ui}}) $$
- $$ {p_{ui}} $$는 상관계수로 edge(u, i)에 대한 decay factor를 의미한다.]
- w1, w2는 학습되는 파라미터
- w2뒤에는 item embedding과 user embedding이 element-wise로 들어가게된다. 이는 유사한 아이템에 대해서 좀더 많은 메세지를 보낼 수 있다는 것이다.
- 앞에 곱해지는 것은 Laplacian norm으로 user와 item 각각의 first-hop 이웃 수 곱의 root를 취한 역수의 값이다. 이는 과거의 아이템이 유저의 선호가 얼마나 기여하는지를 의미한다.(이 부분은 명확히 와닿지가 않았다...)
- 위의 figure에서는 3-order로 그러져있다. 일단 1-order에 대해서 자세히 살펴보면 message construction과 message aggregation이 존재한다
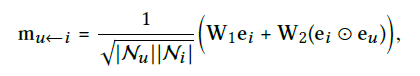
- Message Aggregation
- user의 이웃으로부터 새롭게 표현된 user에 대한 embedding을 concat하는 과정이다.
- 아래의 값은 첫번째 embedding propogation layer를 거치고 나온 user u에 대한 값이다.
- 활성화 함수로는 LeakyRelu를 사용해서 긍정적인 샘플과 부정적인 샘플에 대한 메세지를 받아들인다.
- $$ {m_{u\leftarrow u}} = {W_{1}}{e_{u}}$$로 w1의 가중치는 message construction과 가중치를 공유하며 original feature에 대한 정보를 보존한다.
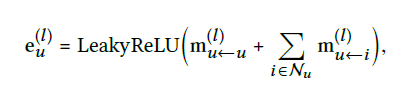

앞서 말했던 message construction과 message aggregation은 다음과 같이 l-layer에 대해서 정의할 수 있다.

또한 3-hop이라고 가정했을 때 u1에 대해서 i4의 message는 위의 그림과 같이 요약될 수 있고
i4 -> u2 -> i2 -> u1에 대한 user-item interaction을 다음과 같이 전달되는것을 확인할 수 있다.
또한 multiple embedding을 쌓아감과 동시에 학습되면서 collaborative signal을 주입할 수 있게 된다.
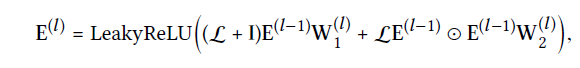
층별 propogation 규칙은 다음과 같은 matrix형태로 제공된다.
E_L은 L 단계 embedding propagation이후 얻어진 user와 item의 embedding을 concat한 결과이다.
I는 identity 행렬이고 L은 라플라시안 행렬로 user-item graph를 아래의 식으로 나타낸것이다.
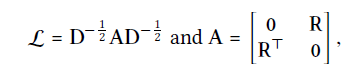
R은 기존의 user-item interaction행렬이고 A는 인접행렬, D는 diagonal 행렬이다.
위의 식은 아래 코드를 통해 수식을 이해하면 편할 것 같아서 참고해주세요!!
def getSparseGraph(self, rating_matrix):
n_users, n_items = rating_matrix.shape
print("loading adjacency matrix")
filename = f'{self.data_name}_s_pre_adj_mat.npz'
try:
pre_adj_mat = sp.load_npz(os.path.join(self.path, filename))
print("successfully loaded...")
norm_adj = pre_adj_mat
except:
print("generating adjacency matrix")
s = time.time()
adj_mat = sp.dok_matrix((n_users + n_items, n_users + n_items), dtype=np.float32)
adj_mat = adj_mat.tolil()
R = rating_matrix.tolil()
adj_mat[:n_users, n_users:] = R
adj_mat[n_users:, :n_users] = R.T
adj_mat = adj_mat.todok()
rowsum = np.array(adj_mat.sum(axis=1))
d_inv = np.power(rowsum, -0.5).flatten()
d_inv[np.isinf(d_inv)] = 0.
d_mat = sp.diags(d_inv)
norm_adj = d_mat.dot(adj_mat)
norm_adj = norm_adj.dot(d_mat)
norm_adj = norm_adj.tocsr()
end = time.time()
print(f"costing {end - s}s, saved norm_mat...")
sp.save_npz(os.path.join(self.path, filename), norm_adj)
- Model Prediction
L layer를 거친 이후에 user에 대한 multiple representation과 item에 대한 multiple representation을 얻을 수 있다.
각 층마다 연결이 다르기 때문에 강조하는 message가 다르기 때문에 final embedding을 얻기위해 각각의 embedding layer를 concat한다. ||는 concat을 의미한다.
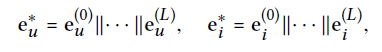
이후 단순 내적을 통해 target item에 대한 user의 선호를 나타냈다.
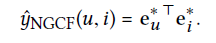
해당 논문에서는 단순 내적을 통해서 간단한 user-item 상호작용을 나타냈는데 neural-network기반 상호작용함수을 통해 조금더 정교한 추천을 하는 방법은 좀 더 연구해야 할 방향성으로 남겨두었다.
- Optimization
model parameter를 학습하기 위해서 해당 논문에서는 추천시스템에서 많이 사용되고 있는 pairwise BPR loss를 선택했다. 해당 loss는 user가 사용한 item과 사용하지 않은 item을 고려하는데 특히 사용한 item에 대해서 많은 반영을 해준다.
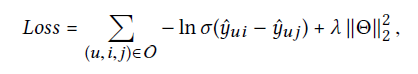
u,i는 긍정적인 item, u,j는 부정적인 item을 의미한다. 둘의 차이에서 sigmoid함수를 태우고 이후 자연로그를 씌운다.
각각의 embedding값과 w1, w2는 모두 학습 되어지는 parameter이다. 또한 뒤에 L2 정규화를 함으로써 과적합을 방지했다.
이번에도 코드를 첨부할테니 참고하길 바랍니다!!
positive / negative pairwise class입니다
class PairwiseGenerator:
def __init__(self, input_matrix, num_negatives=1, batch_size=32, shuffle=True, device=None):
super().__init__()
self.input_matrix = input_matrix
self.num_negatives = num_negatives
self.num_users, self.num_items = input_matrix.shape
self.batch_size = batch_size
self.shuffle = shuffle
self.device = device
self._construct()
def _construct(self):
self.pos_dict = {}
for u in range(self.num_users):
u_items = self.input_matrix[u].indices
self.pos_dict[u] = u_items.tolist()
def __len__(self):
return int(np.ceil(self.num_users / self.batch_size))
def __iter__(self):
if self.shuffle:
perm = np.random.permutation(self.num_users)
else:
perm = np.arange(self.num_users)
for b, st in enumerate(range(0, len(perm), self.batch_size)):
batch_pos = []
batch_neg = []
ed = min(st + self.batch_size, len(perm))
batch_users = perm[st:ed]
for i, u in enumerate(batch_users):
posForUser = self.pos_dict[u]
if len(posForUser) == 0:
continue
posindex = np.random.randint(0, len(posForUser))
positem = posForUser[posindex]
while True:
negitem = np.random.randint(0, self.num_items)
if negitem in posForUser:
continue
else:
break
batch_pos.append(positem)
batch_neg.append(negitem)
batch_users = torch.tensor(batch_users, dtype=torch.long, device=self.device)
batch_pos = torch.tensor(batch_pos, dtype=torch.long, device=self.device)
batch_neg = torch.tensor(batch_neg, dtype=torch.long, device=self.device)
yield batch_users, batch_pos, batch_neg
다음으로 ngcf가 진행되는 전진 패스 과정입니다. embedding 생성부터 bpr loss까지 잘 나타나있으니 위에 말이 이해가 되지 않았더라면 코드를 보고 이해하시길 바랍니다
def forward(self, u, i, j):
"""
Computes the forward pass
Arguments:
---------
u = user
i = positive item (user interacted with item)
j = negative item (user did not interact with item)
"""
# dropout 적용
if self.node_dropout > 0.:
self.A_hat = self._droupout_sparse(self.A)
ego_embeddings = torch.cat([self.weight_dict['user_embedding'], self.weight_dict['item_embedding']], 0)
all_embeddings = [ego_embeddings]
# forward pass n번째 propagation layers
for k in range(self.n_layers):
if self.node_dropout > 0.:
side_embeddings = torch.sparse.mm(self.A_hat, ego_embeddings)
else:
side_embeddings = torch.sparse.mm(self.A, ego_embeddings)
# transformed sum weighted sum messages of neighbors
sum_embeddings = torch.matmul(side_embeddings, self.weight_dict['W_gc_%d' % k] + self.weight_dict['b_gc_%d' % k])
sum_embeddings = F.leaky_relu(sum_embeddings)
# bi messages of neighbours
bi_embeddings = torch.mul(ego_embeddings, side_embeddings)
# transformed bi messages of neighbours
bi_embeddings = torch.matmul(bi_embeddings, self.weight_dict['W_bi_%d' % k] + self.weight_dict['b_bi_%d' % k])
bi_embeddings = F.leaky_relu(bi_embeddings)
ego_embeddings = sum_embeddings + bi_embeddings
mess_dropout_mask = nn.Dropout(self.mess_dropout)
ego_embeddings = mess_dropout_mask(ego_embeddings)
# normalize activation
norm_embeddings = F.normalize(ego_embeddings, p=2, dim=1)
all_embeddings.append(norm_embeddings)
all_embeddings = torch.cat(all_embeddings, 1)
# back to user/item dimension
u_g_embeddings, i_g_embeddings = all_embeddings.split([self.n_users, self.n_items], 0)
self.u_g_embeddings = nn.Parameter(u_g_embeddings)
self.i_g_embeddings = nn.Parameter(i_g_embeddings)
u_emb = u_g_embeddings[u] # user embeddings
p_emb = i_g_embeddings[i] # positive item embeddings
n_emb = i_g_embeddings[j] # negative item embeddings
y_ui = torch.mul(u_emb, p_emb).sum(dim=1)
y_uj = torch.mul(u_emb, n_emb).sum(dim=1)
log_prob = (torch.log(torch.sigmoid(y_ui-y_uj))).mean()
# compute bpr-loss
bpr_loss = -log_prob
if self.reg > 0.:
l2norm = (torch.sum(u_emb**2)/2. + torch.sum(p_emb**2)/2. + torch.sum(n_emb**2)/2.) / u_emb.shape[0]
l2reg = self.reg*l2norm
bpr_loss = -log_prob + l2reg
return bpr_lossPyTorch에서 신경 그래프 협업 필터링 구현
Neural Graph Collaborative Filtering (NGCF)은 Wang 등이 개발 한 딥 러닝 추천 알고리즘입니다. (2019)는 임베딩을 전파하여 사용자 항목 그래프 구조를 활용합니다.
ichi.pro
자세한 코드는 아래 깃헙을 참고해주세요~
github.com/bladejun/Recommend_System_Pytorch
bladejun/Recommend_System_Pytorch
Recommend System Model by Pytorch. Contribute to bladejun/Recommend_System_Pytorch development by creating an account on GitHub.
github.com
'추천 시스템 논문' 카테고리의 다른 글
| code로 보는 TransR 논문 (0) | 2021.05.19 |
|---|---|
| LightGCN 논문 리뷰 (0) | 2021.03.29 |
| code와 함께 보는 TransH 논문 리뷰 (0) | 2021.03.26 |
| code와 함께 보는 TransE 논문 리뷰 (0) | 2021.03.16 |
| Deep Neural Networks for YouTube Recommendation (0) | 2021.01.17 |




댓글