논문: Wang, Zhen, et al. "Knowledge graph embedding by translating on hyperplanes."
code: github.com/bladejun/Knowledge_graph_tensorflow
bladejun/Knowledge_graph_tensorflow
Knowledge Graph Embedding Model collections implemented by TensorFlow - bladejun/Knowledge_graph_tensorflow
github.com
TransH는 TransE의 단점을 해결하기위해서 hyperplane을 이용해서 새롭게 제안한 알고리즘이다.
bladejun.tistory.com/91?category=426400
code와 함께 보는 TransE 논문 리뷰
논문: Bordes, Antoine, et al. "Translating embeddings for modeling multi-relational data." 코드: github.com/bladejun/Knowledge_graph_tensorflow bladejun/Knowledge_graph_tensorflow Knowledge Graph Em..
bladejun.tistory.com
그럼 TransE의 단점을 먼저 살펴보겠습니다. TransE를 잘 모르시는 분들은 위에 내용을 먼저 살펴봐주세요!
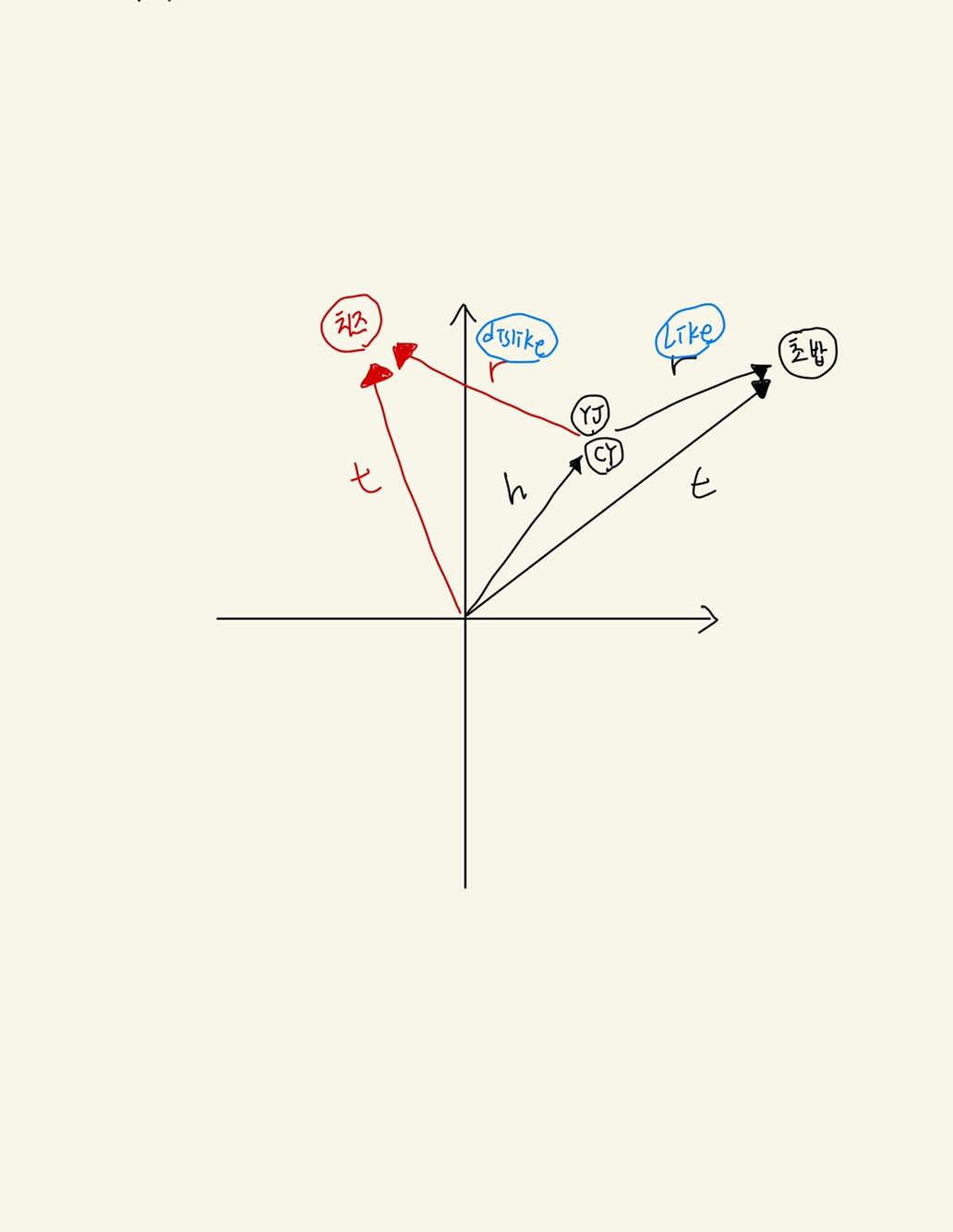
(h, r, t)관계를 표시할때 (YJ, Like, 초밥), (CY, Like, 초밥) triplet을 표현하면 두 entity는 동일한 relation과 tail이기 때문에 비슷한곳에 embedding이 됩니다. 하지만 (YJ, dislike, 치즈)라는 triplet이 있다면 YJ는 CY와는 다르게 하나의 관계가 더 표현됩니다. 즉 YJ는 2개의 relation에 속하는 entitiy입니다. 이렇게 될 경우 TransE를 바탕으로 진행하면 CY의 relation을 강제로 치즈를 싫어하게 만들어버립니다. 이러한 문제점 즉, 1:N, N:1, N:N관계를 TransE에서는 해결하지 못하기 때문에 hyperplane을 도입해서 YJ와 CY의 distance의 차이를 만들면서 TransH라는 새로운 알고리즘을 제안했다.

간략하게 TransE와 TransH의 illustration을 위와 같이 표시했다. TransE의 경우 (h, r, t)를 바로 embedding시켰다면 TransH에서는 새로운 초평면에 투영시켜서 mapping시켰다는 차이점이 있다. 결국 TransE에서 해결하지 못했던 "동일 entity가 여러 relation에서 구분이 안된다"는 문제를 초평면을 도입시킴으로써 해결했다.
결국 scoring function은 다음과 같이 정의된다. ||w_r||2 = 1로 가정하고 정의했다.
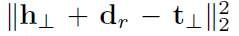


code
def _score_func(self, h, r, t):
"""f_r(h,t) = |(h-whw)+d_r-(t-wtw)|, w_r,d_r is orthogonal."""
self.w = tf.get_variable("Mr", [1, 1, self.k])
self.w = tf.tile(self.w, [self.batch_size, 1, 1]) # (batch_size, 1, embedding_dimension)
h = tf.expand_dims(h, axis=2) # (batch_size, embedding_dimension) -> (batch_size, embedding_dimension, 1)
t = tf.expand_dims(t, axis=2) # (batch_size, embedding_dimension) -> (batch_size, embedding_dimension, 1)
h_v = tf.squeeze(h, axis=2) - tf.squeeze(tf.matmul(self.w, tf.matmul(h, self.w)), axis=1)
t_v = tf.squeeze(t, axis=2) - tf.squeeze(tf.matmul(self.w, tf.matmul(t, self.w)), axis=1)
distance = h_v + r - t_v
if self.params.score_func.lower() == 'l1': # L1 score
score = tf.reduce_sum(tf.abs(distance), axis=1)
elif self.params.score_func.lower() == 'l2': # L2 score
score = tf.sqrt(tf.reduce_sum(tf.square(distance), axis=1))
return score
'추천 시스템 논문' 카테고리의 다른 글
| code로 보는 TransR 논문 (0) | 2021.05.19 |
|---|---|
| LightGCN 논문 리뷰 (0) | 2021.03.29 |
| code와 함께 보는 TransE 논문 리뷰 (0) | 2021.03.16 |
| Neural Graph Collaborative Filtering (0) | 2021.02.05 |
| Deep Neural Networks for YouTube Recommendation (0) | 2021.01.17 |




댓글