- 문제 설명
XX 게임에서는 지형 편집 기능을 이용하여 플레이어가 직접 게임 속 지형을 수정할 수 있습니다. 이 게임에서는 1 x 1 x 1 크기의 정육면체 블록을 쌓아 게임 속 지형을 표현합니다. 이때, 블록이 공중에 떠 있거나, 블록 하나가 여러 개의 칸에 걸쳐 놓일 수는 없습니다. 따라서 지형을 편집하기 위해서는 각 칸의 제일 위에 블록 1개를 새로 추가하거나, 제일 위에 있는 블록 한 개를 삭제하는 방식으로 지형을 수정해야 합니다. 이때, 블록 한 개를 새로 추가하거나 삭제하기 위해서는 게임머니를 사용해야 하므로 몇 개의 블록을 추가하고 삭제할지 신중한 선택이 필요합니다.
이 게임을 즐기던 한 플레이어는 N x N 크기의 지역에 자신만의 별장을 만들고 싶어졌습니다. 이를 위해서는 울퉁불퉁한 지형의 모든 칸의 높이가 같아지도록 만들어야 합니다. 이때, 블록 한 개를 추가하려면 P의 비용이, 제거하려면 Q의 비용이 들게 됩니다.
다음은 블록 한 개를 추가할 때 5의 비용이, 제거할 때 3의 비용이 드는 경우, 3 x 3 넓이의 모든 칸의 블록 높이가 같아지도록 만드는 예시입니다.

위 그림과 같이 지형 블록이 놓여 있는 경우 모든 칸의 높이가 3으로 같아지도록 한다면 다음과 같은 모양이 됩니다.
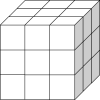
이를 위해서는 3보다 높은 칸의 블록 2개를 제거하고, 3보다 낮은 칸에 총 8개의 블록을 추가해야 하며, 2 x 3 + 8 x 5 = 46의 비용이 들게 됩니다.
그러나 아래 그림과 같이 모든 칸의 높이가 2로 같아지도록 할 때는 6개의 블록을 제거하고, 3개의 블록을 추가하면 6 x 3 + 3 x 5 = 33의 비용이 들게 되며, 이때가 최소비용이 됩니다.

현재 지형의 상태를 나타내는 배열 land와 블록 한 개를 추가하는 데 필요한 비용 P, 블록 한 개를 제거하는 데 필요한 비용 Q가 매개변수로 주어질 때, 모든 칸에 쌓여있는 블록의 높이가 같아지도록 하는 데 필요한 비용의 최솟값을 return 하도록 solution 함수를 완성해 주세요.
- 제한사항
- land는 N x N 크기의 2차원 배열이며, N의 범위는 1 ≤ N ≤ 300입니다.
- land의 각 원소는 각 칸에 놓여 있는 블록의 수를 나타내며, 0 이상 10억 이하의 정수입니다.
- 각 칸에 블록 하나를 추가하는 데는 P, 제거하는 데는 Q의 비용이 들며, P, Q의 범위는 1 ≤ P, Q ≤ 100인 자연수입니다.
- 입/출력
| land | P | Q | result |
| [[1, 2], [2, 3]] | 3 | 2 | 5 |
| [[4, 4, 3], [3, 2, 2], [ 2, 1, 0 ]] | 5 | 3 | 33 |
- 코드
def solution(land, P, Q):
lst = []
for i in land:
lst += i
lst = sorted(lst)
n = len(lst)
answer = sum(lst)*Q
cost = (sum(lst) - lst[0]*n )*Q
answer = min(answer, cost)
for i in range(1, n):
if lst[i] != lst[i-1]:
cost += (P * i * (lst[i]-lst[i-1])) - (Q * (n-i) * (lst[i]-lst[i-1]))
answer = min(answer, cost)
return answer1) 기존의 값을 하나의 리스트로 만들고 오름차순으로 정리를 해준다.
2) answer = sum(lst)*Q -> 전부 다 0층일때의 값
3) sum(lst) - lst[0]*n)*Q -> 첫번째 층의 값을 기준으로 지형을 맞췄을때 드는 비용
전체의 개수에서 맨 밑에줄은 전부다 블록이 있기 때문에 해당개수를 빼준다.
4) lst[i] != lst[i-1] -> 그 이후에 값을 진행하면서 높이가 달라질때
5) i번쨰 index를 기준으로 왼쪽은 블록의 높이가 낮기때문에 P(블록을 쌓는데 드는 비용) * i(블록을 쌓아야할 개수) * lst[i]-lst[i-1](블록의 높이)은 더해주고
6) 현재 lst[i]블록 높이 기준으로 맞추는것이기 때문에 밑에 공식은 제거 대상이 아니기 때문에 전체 제거해야할 대상(sum(lst))에서 빼준다.
Q(블록을 제거하는데 드는 비용) * n-i(블록을 제거해야할 개수) * lst[i]-lst[i-1](블록의 높이)
<초기 지형>
| O | |||
| O | O | O | |
| O | O | O | O |
cost = 전체 제거한다면 8개 * 2(제거비용) = 16
<i=0>
| O | |||
| O | O | O | |
| O | O | O | O |
첫번째를 기준으로 지형의 높이를 맞추면 16 - 4*2(첫번째층 제거불필요하기 때문에 빼준다) = 8
8은 즉, 1층을 제외한 나머지 블록 4개 * 2(제거비용)=8이라고 보는것이다.
cost = 16-8=8
<i=1>
| O | |||
| X | O | O | O |
| O | O | O | O |
맨 밑에 층은 이미 cost에서 빠졌기 때문에 고려할 필요가 없다
i=1일때 기준으로 지형의 높이를 맞추면 1번째열(빨간색)은 블록이 추가되어야해서 비용을 더해주고 2~4번째열(파란색)은 블록이 제거 불필요해서 비용을 제거해야한다.
빨간색 -> 1(추가개수) * 3(추가비용) * 1(블록높이=(2-1))
파란색 -> 3(제거개수) * 2(제거비용) * 1(블록높이=(2-1))
cost = 8+3-6=5(즉, 1열에서 1개추가 비용(3) + 4열에서 1개 제거비용(2) = 5와 동일하다)
<i=2>
| X | X | X | O |
| X | O | O | O |
| O | O | O | O |
i=2일때 기준으로 지형의 높이를 맞추면 1,2,3번째열(빨간색)은 블록이 추가되어야해서 비용을 더해주고 4번째열(파란색)은 블록이 제거 불필요해서 비용을 제거해야한다.
빨간색 -> 3(추가개수) * 3(추가비용) * 1(블록높이=(2-1))
파란색 -> 1(제거개수) * 2(제거비용) * 1(블록높이=(2-1))
cost = 5+9-2=12(즉, 빨간색 4개 추가비용=12와 동일하다)
- 출처
https://programmers.co.kr/learn/courses/30/lessons/12984?language=python3
'알고리즘' 카테고리의 다른 글
| 프로그래머스 자동 완성 (python, 파이썬) (4) | 2021.05.24 |
|---|---|
| 프로그래머스 110 옮기기 (python, 파이썬) (0) | 2021.05.22 |
| 프로그래머스 스티커 모으기 (python, 파이썬) (0) | 2021.05.14 |
| 프로그래머스 점프와 순간이동 (python, 파이썬) (0) | 2021.05.14 |
| 프로그래머스 단어 퍼즐 (python, 파이썬) (0) | 2021.05.13 |

댓글